
안녕하세요. 오늘은 초등수학 6학년 2학기 비례식과 비례배분 2번째 시간입니다.
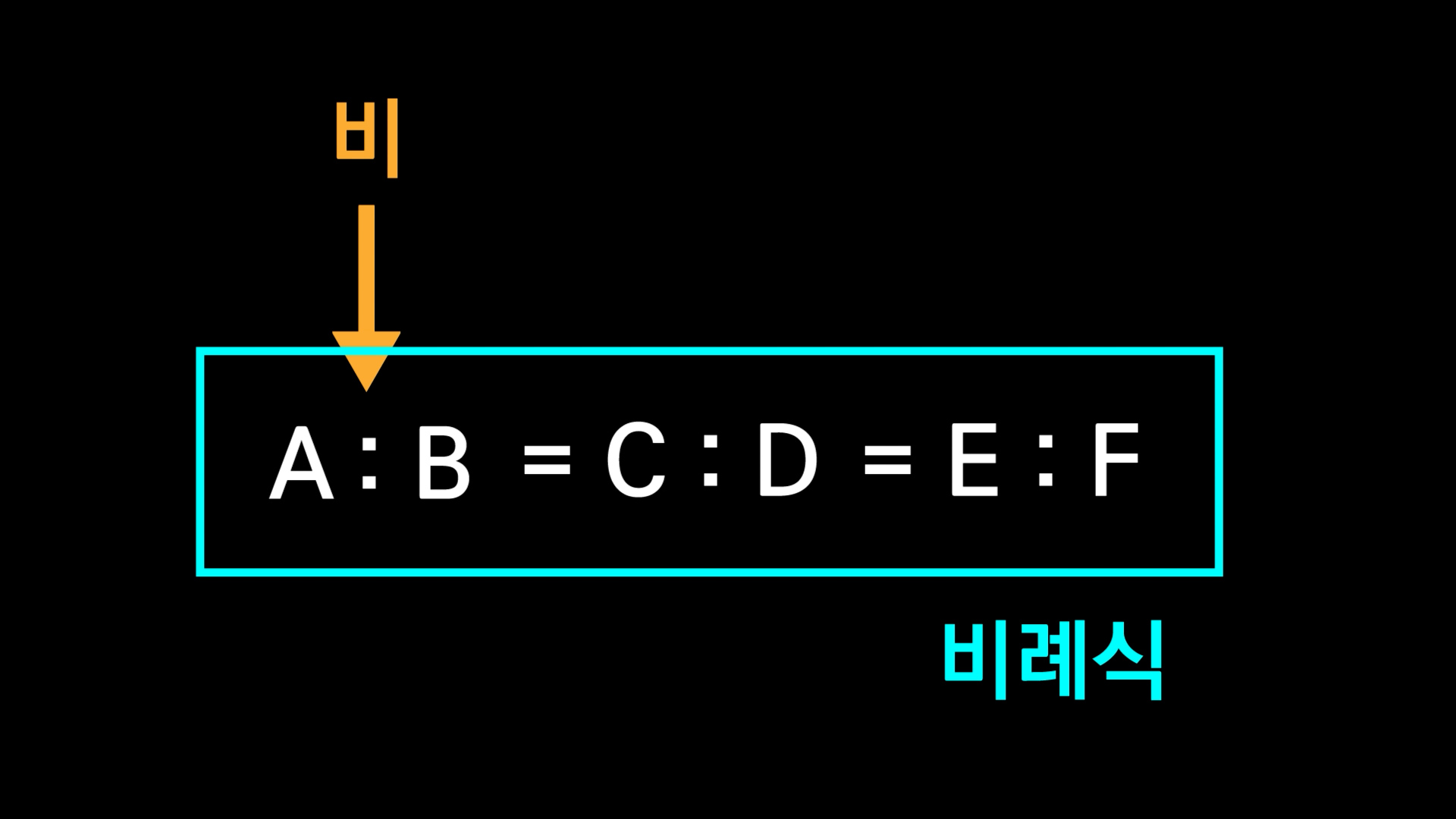
이렇게 몇대 몇이라고 쓰면서 쌍점 양쪽을 비교하는 것을 보고 ‘비’라고 한다고 했죠?
이 비를 등호를 사용해서 연결한 것을 비례식이라고 합니다.
비례식과 비례배분 1에서 물통에 든 물을 예로 들면서 6:12가 3:6이 되기도 하고 1:2가 되는 걸 봤죠?
이제 이걸 이렇게 등호를 써서 6:12 = 3:6 = 1:2라고 쓸 수 있게 된 겁니다. 물론 아무 거나 등호로 연결할 수 없다는 건 아시죠?
이 6:12, 3:6, 1:2는 전항과 후항에 나누기 2를 하거나, 나누기 3을 해서 변한 것이라고 볼 수도 있고, 1:2부터 시작하면 곱하기 3, 곱하기 2를 한 것이잖아요. 이렇게 전항과 후항에 같은 수로 곱하거나 나누기를 해서 변한 것은 같다고 할 수 있죠. 즉, 등호를 연결할 수 있는데요.
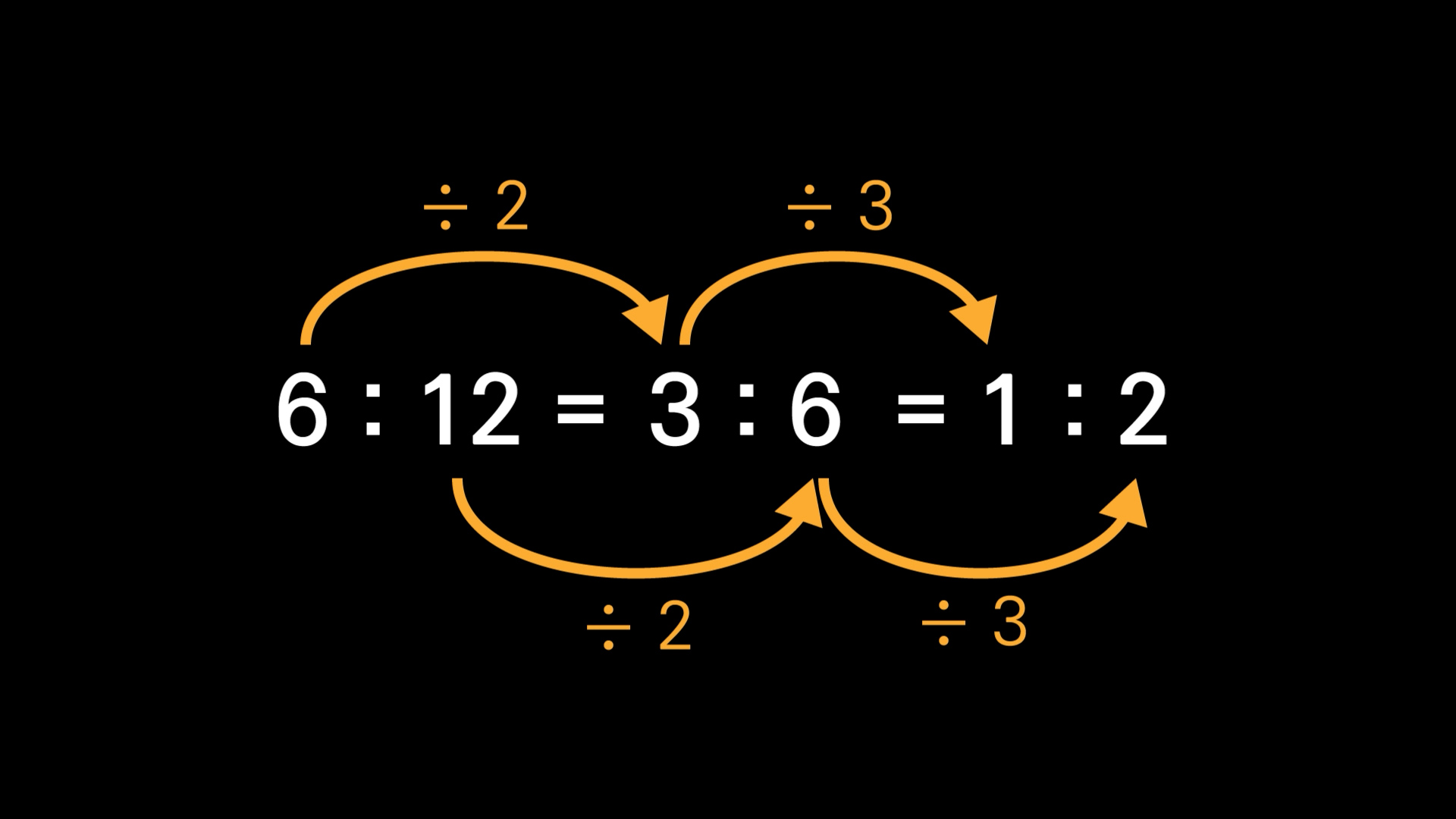
그 외에 것들 예를 들어 전항과 후항에 같은 수를 더한 것 가령 1:2의 전항과 후항에 4를 더해서 5:6을 만든 것은 같은 것이 아니다.. 라고 배웠죠?
다른 수를 곱한 거나 나눈 것도 마찬가지입니다. 1:2에 전항은 2를 곱하고 후항엔 3을 곱해서 2:6을 만든다면 이건 앞의 것과 같지 않습니다. 등호로 연결할 수 없죠.
오직 전항과 후항에 같은 수를 곱하거나 나누는 경우에만 등호를 연결할 수 있다는 걸 기억합시다.
이렇게 전항과 후항에 똑같은 수를 곱하거나 나눠도 비가 변하지 않는 성질은 마치 분수를 떠올리게 합니다. 분수도 분자, 분모에 똑같은 수를 곱하거나 나눠도 분수가 변하지 않죠? (6/12 = 3/6 = 1/2)
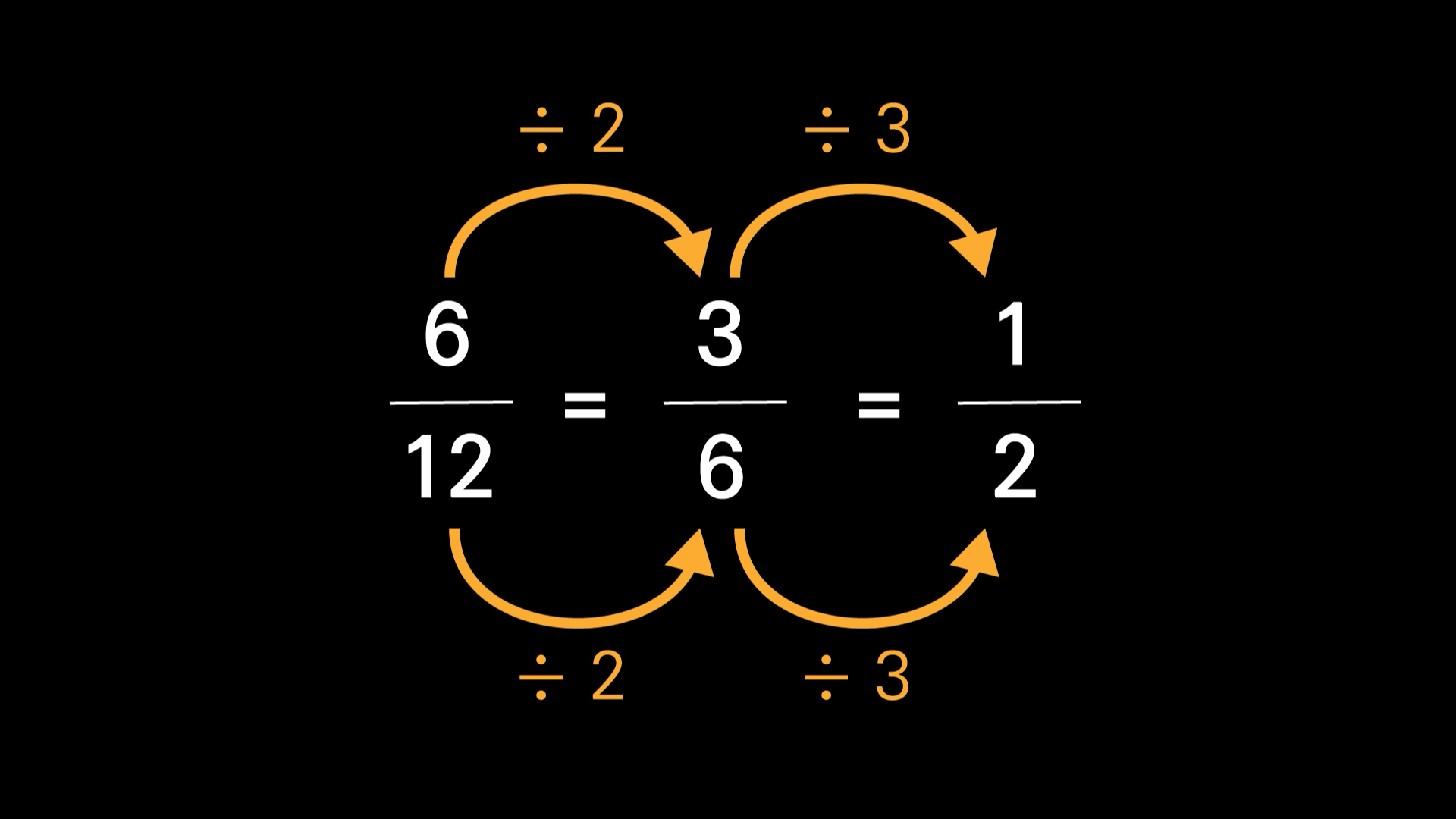
그래서 비를 이야기할 때 1:2야 라고 하기도 하지만 이걸 분수로 표현하기도 합니다. 1/2 이렇게요.
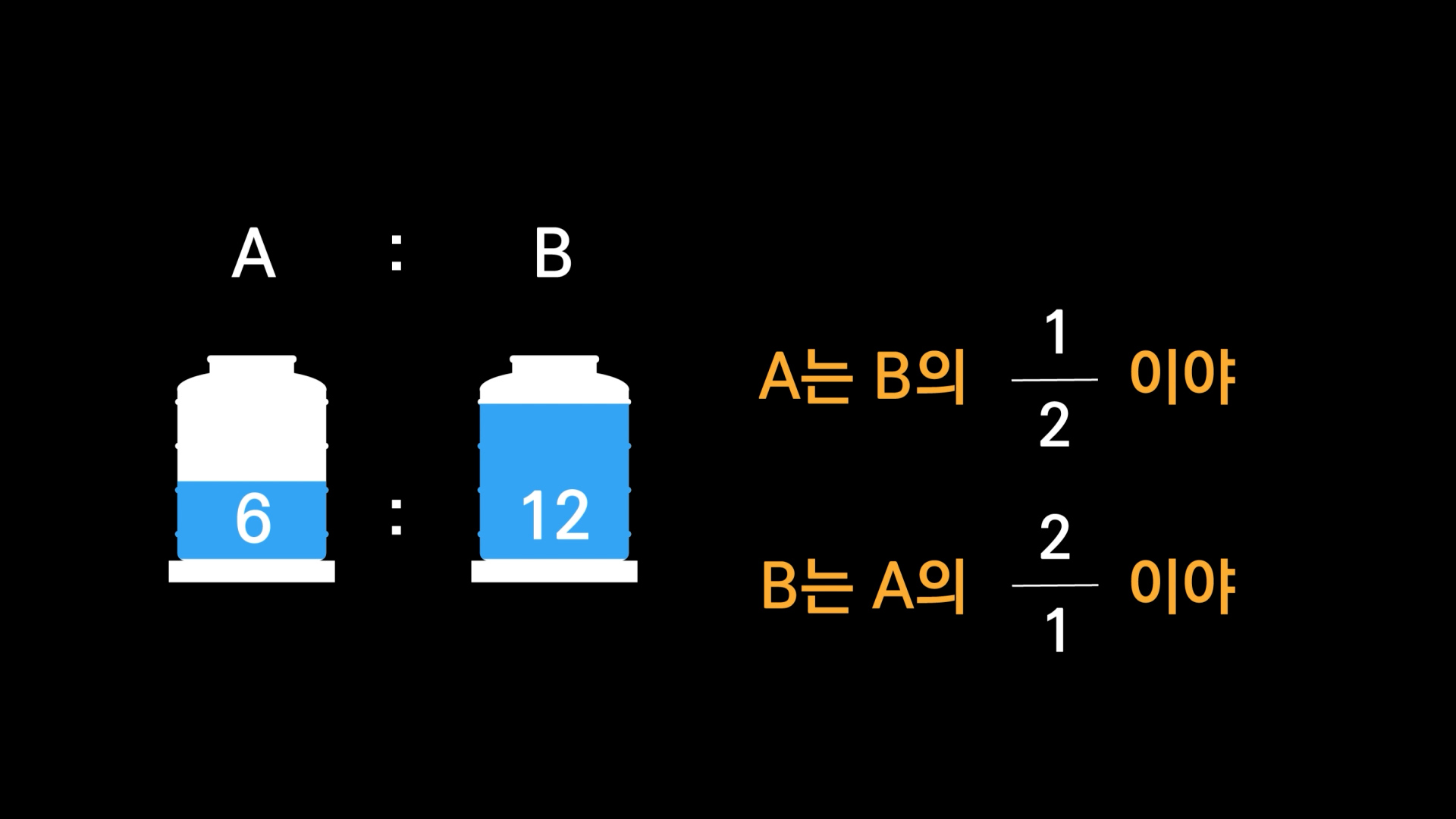
그래서 지난 번 썼던 물통의 예를 들어보면요. A 물통은 6리터, B물통은 12리터가 들어있잖아요. A물통과 B물통의 비, 비율은 어떻게 되? 라고 물으면 뭐라고 답하면 되겠어요? 비를 써서 6대 12야 라고 해도 된다고 배웠죠. 그렇게 얘기할 수도 있고, A물통을 분자, B물통을 분모에 놓으면, A물통은 B물통의 6/12야, 혹은 3/6 혹은 1/2야 라고 얘기해도 다 맞습니다.
거꾸로 A물통을 분모에 B물통을 분자에 놓으면, 12/6 = 6/3 = 2/1이 되어서 B물통은 A의 두 배야라고 할 수있게 되는 거죠.
비 두개를 연결했을 때, 가령 3:6 = 1:2 에서 바깥쪽에 있는 3과 2를 보고 바깥 외자를 써서 외항. 6과 1은 안쪽에 있다고 해서 내항이라고 합니다. 이 내항과 외항은 중요한 성질이 있는데요. 바로 ‘외항의 곱과 내항의 곱’은 항상 같다는 겁니다.

이런 건 어디에 쓰냐면요?
2:5 = 4: 네모 처럼 비례식의 하나가 비어 있을 때 이 네모를 알아내기 위해서 이 성질을 써요.
자 외항 끼리의 곱과 내항끼리의 곱이 같다고 했죠?
여기서 외항끼리의 곱은 2와 네모의 곱이 되고 내항의 곱은 5 곱하기 4 그래서 20이 됩니다.
그럼 네모는 뭐여야 2를 곱하면 20이 될까요? 양쪽을 2로 나누면 네모는 10이 되는 거죠.

또 비례식의 외항의 곱과 내항의 곱이 같다는 건 비례식이 맞는지 틀리는지를 가리는데도 쓸 수 있겠죠?
가령 1:2=4:5라는 비례식이 있다고 해보죠. 이걸 외항의 곱과 내항의 곱을 비교하면 외항의 곱은 5이고 내항의 곱은 8이 잖아요. 그러면 알 수 있죠. 아, 이건 틀린 비례식이구나. 등호가 아니라 부등호로 연결해야 하는 거구나, 알 수 있죠.

자 그럼 비례식을 이용해서 문제를 풀어볼까요? 전에 분수의 나눗셈에서 했던 문제입니다.
수학 문제 6문제를 푸는데 3/5 시간이 걸렸을 때 1시간 동안 풀 수 있는 문제 수 구하기
자 이런 문제도 이제는 비례식을 통해서 쉽게 풀 수 있습니다. 그 방법을 알려드릴게요.
우선 어떤 종류의 숫자가 있는지 정리해 보죠. 6이란 숫자는 문제 수죠. 그리고 3/5 이라는 숫자는 시간이고요. 3/5시간에 6문제를 풀었다는 건 이미 알고 있는 겁니다. 우리가 모르는 건 한 시간이란 시간 동안 몇 문제를 풀 수 있느냐죠? 이건 네모로 적을게요.
우선 이걸 비로 만들죠. 그리고 이걸 등호로 연결해 비례식으로 만듭니다. 왜 등호로 연결할 수 있냐고요? 그건 같은 속도로 문제를 풀 거기 때문에 그래요. 그래서 6:3/5 = 네모 :1이 되는 거죠.
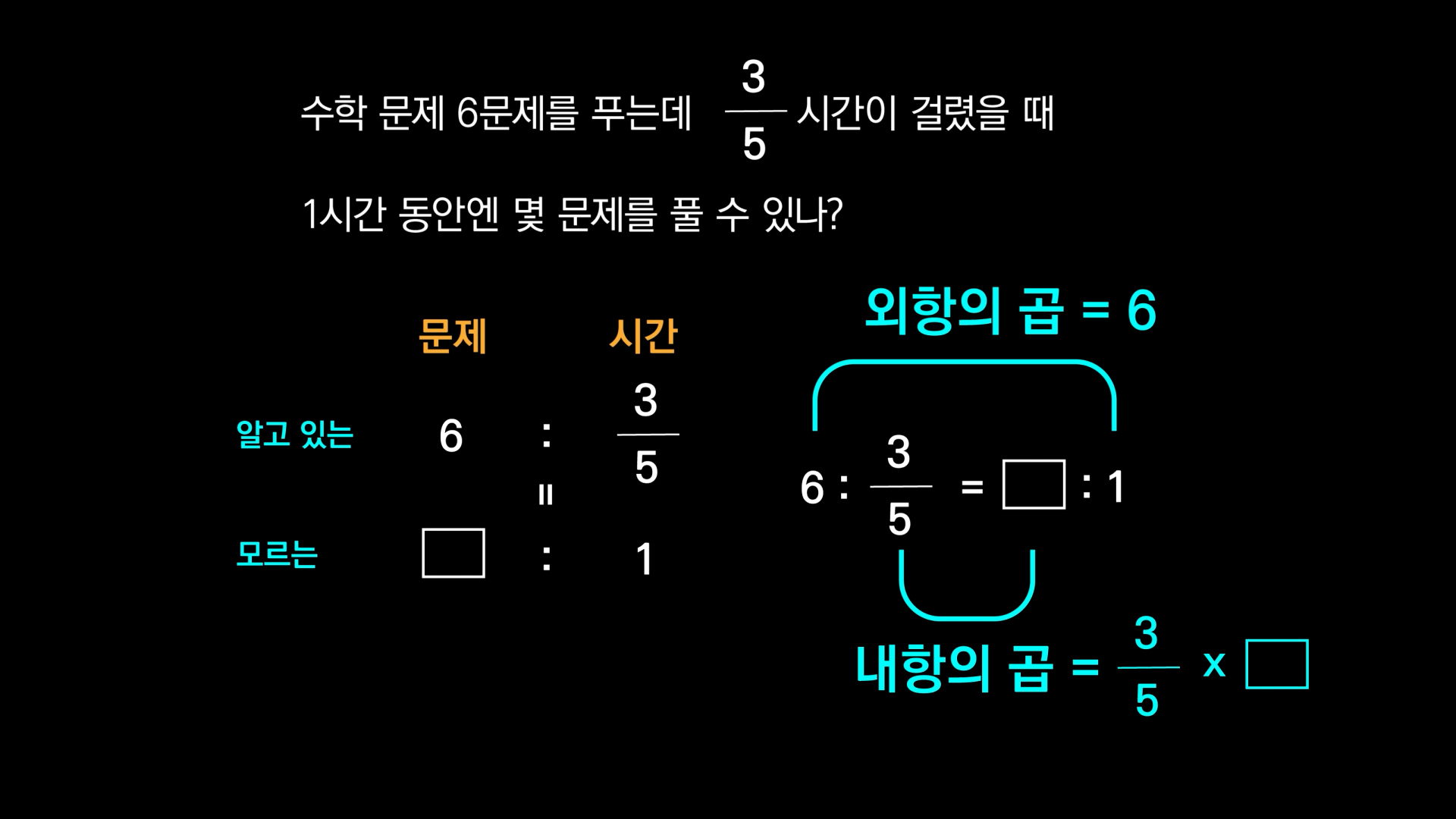
이걸 외항의 곱과 내항의 곱을 구해서 같다고 하면 3/5곱하기 네모 = 6이 되는 거죠.
네모 쪽에 3/5가 거슬리죠? 이게 없어야 네모를 구할 수 있는데요.
그래서 양변에 똑같이 3/5의 역수 5/3를 곱해주면, 네모는 10이 되는 거죠. 즉, 1시간이면 10문제를 풀 수 있다는 얘기가 됩니다.

자, 오늘의 마지막 비례배분에 대해서 알아보겠습니다.
우리가 일상생활에서 몇 대 몇으로 나누자라는 말을 종종 쓰거든요. 이걸 비례배분이라고 합니다.
가령 어떤 사람이 귤이 있는데 50개나 땄어요. 이걸 A와 B가 2:3으로 나누자라고 하면 몇 개씩 나누면 될까요? 다시 얘기하면 전체 50개의 몇 분의 몇 씩 가져가면 될까요? 어떤 학생은 금방 답을 찾기도 했을 텐데요. 어떤 학생은 잘 모르겠죠.

그러면 전체 숫자를 가장 쉽게 바꿔보는 겁니다. 가장 쉬운 건 비의 전항과 후항을 더한 수부터 생각하는 겁니다. 여기서는 뭐죠? 전항이 2고 후항이 3이니, 둘을 합치면 5죠. 그럼 귤이 5개 있다고 생각하는 겁니다. 그러면 이걸 A와 B가 2:3으로 나누면 몇개씩 나눈다는 거죠? 그렇죠. A가 2개, B가 3개 갖는다는 얘깁니다.
이렇게 보면 A는 지금 전체가 다섯개니까 2개를 가졌지만 전체의 2/5개를 갖고, B는 다섯개 중의 3개를 가졌지만 전체의 3/5를 갖는다고 할 수 있죠. 비례식에서 전항과 후항에 1/5을 같이 곱해주면 되니까 이렇게 쓸 수 있을 겁니다.

비례배분은 이렇게 비율을 분수로 표현해주는 것이 중요해요. 이때 분모는 전항과 후항의 합입니다. 이제 남은 것은 전체 숫자를 각각 곱해주면 A가 갖는 귤, B가 갖는 귤이 나옵니다. 즉, A는 50개의 2/5 즉, 50 곱하기 2/5해서 20개, B는 50개의 3/5, 즉 50 곱하기 3/5해서 30개가 되는 거죠.
자 기억합시다. 비율대로 나누는 것이 비례배분인데요. 이때는 비율을 전항과 후항의 합계를 분모로 만든 분수로 만들고, 이 분수를 전체 크기에 곱하면 됩니다.

'초등수학' 카테고리의 다른 글
| 원의 넓이 01 (6-2) (0) | 2022.10.09 |
|---|---|
| 비례식과 비례배분 01 (6학년) (0) | 2022.08.28 |
| 소수의 나눗셈 01 (6학년) (0) | 2022.08.15 |
| 분수의 나눗셈 02 (0) | 2021.02.27 |
| 분수의 나눗셈 01 (6학년) (0) | 2021.02.21 |



