안녕하세요. 루타입니다. 오늘은 원에 대해서 다뤄보겠습니다. 초등수학 6학년 2학기 과정이죠.
‘원’이라고 하면 뭘 말하는 걸까요? 네 바로 ‘동그라미’입니다. 동그라미를 정확히 그리려면 어떻게 그리면 될까요? 컴파스라는 도구를 쓰는 거죠? 이렇게요.

아니면 실에 연필을 달아서 한쪽을 움직이지 않게 누르고 돌리면 원이 나올 겁니다.

https://www.wikihow.com/Draw-a-Circle
6 Ways to Draw a Circle - wikiHow
Drawing a circle freehand is tricky, but luckily there are lots of tools and tricks at your disposal that can help. From using a compass to tracing round objects, drawing perfect circles will be a breeze once you find the method that works...
www.wikihow.com
이 원에서 원의 둘레를 ‘원주’라고 부르고요. 컴파스의 바늘을 찍었던 점을 ‘원의 중심’이라고 부르기로 하죠. 또 ‘원의 중심’을 지나면서 ‘원주’ 양쪽을 잇는 선을 ‘원의 지름’이라고 합니다. 그리고 중심에서 원주까지의 거리는 지름의 반이라고 해서 ‘반지름’이라고 합니다.
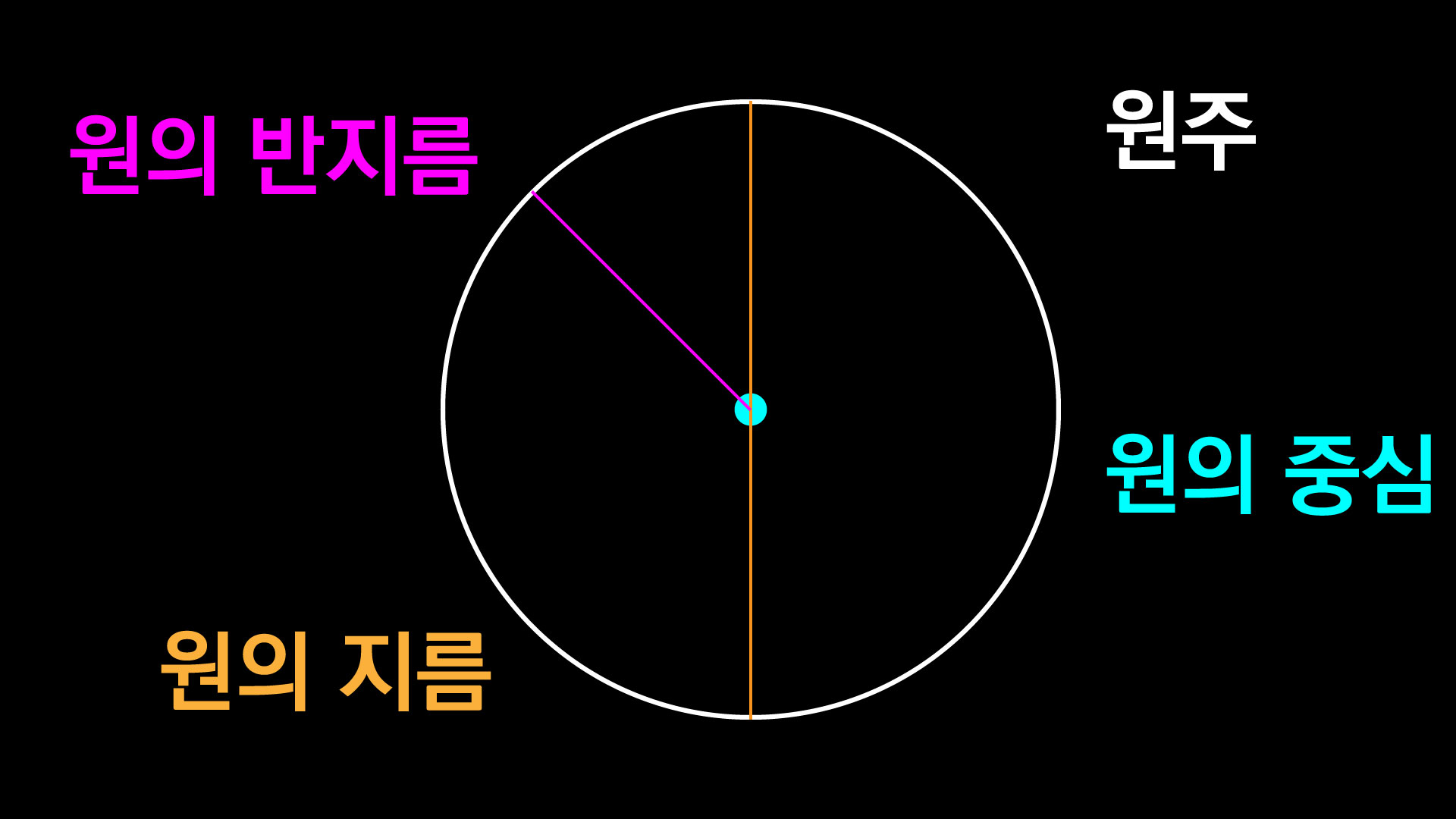
이제 이렇게 이름을 붙이면 원의 크기를 비교할 수 있겠죠? A라는 원의 지름은 5cm야. B라는 원의 지름은 3cm야라고 하면 우리가 그림을 보지 않더라도 ‘아, A라는 원이 B라는 원보다 더 크구나’라는 것을 알 수 있을 거예요.

원의 ‘지름’과 원의 ‘원주’ 사이의 관계
우리가 언뜻 보기에도 지름도 커지면, 원도 커지고 원주도 커진다는 것을 알 수 있죠? 분명히 원의 둘레 ‘원주’는 ‘지름’보다 몇 배 크다고 표시할 수 있을 것 같은데, 진짜 몇 배가 될까요? 한 세 배? 네 배?
이렇게 생각해 볼게요. 원의 지름과 중심 길이가 같은 정육각형을 그려볼까요? 그러면 이 원의 반지름이 정육각형을 이루는 6개의 정삼각형의 한 변의 길이가 되는 거죠? 정육각형의 둘레는 이 반지름의 여섯배입니다. 지름은 반지름의 두 배니까 정육각형의 둘레는 지름의 세 배인 거죠. 여기서 우리가 원의 둘레 원주는 정확히 알지 못하지만 정육각형보다 먼 거리를 돌아가니까 정육각형의 둘레보다 원주가 더 크다고 할 수 있죠? 즉, 원의 지름 곱하기 3보다 원주가 크다는 거죠.

이번엔 지름과 길이가 같은 변을 갖는 정사각형을 그려볼까요? 그러면 이 사각형의 한변의 길이는 원의 지름이 되고, 둘레는 어떻게 되죠? 지름의 네 배가 됩니다. 그런데 이 정사각형의 둘레는 원의 둘레 바깥쪽을 멀리 돌아가니까 원주보다 정사각형의 둘레가 더 크죠. 즉, 원의 지름 곱하기 4보다 원주가 작다는 얘깁니다.

정리하면 원주는 원의 지름 곱하기 3보다 크고, 원의 지름 곱하기 4보다 작다고 할 수 있죠.
그럼 진짜 원주는 원의 지름에 몇을 곱하면 나올까요? 수학자들이 조사를 해봤는데요. 아쉽게도 딱 떨어지는 수는 아니었습니다. 세 배보다 약간 큰 3.14159265358979… 이렇게 계속 나간다고 해요. 즉, 지름에 3.141592…를 곱하면 원의 둘레 ‘원주’가 나오는 거죠. 맨날 이렇게 복잡한 수를 곱할 수는 없으니까요. 우리는 둘째자리에서 반올림해서 3.1이라고 하기로 하죠. 이 3.1에 지름을 곱하면 원주가 나오기 때문에, 원주율이라고 부릅니다.

이제 우리는 지름만 알면 이 원주율을 가지고 쉽게 원주를 구하게 됐어요. 만약 어느 원의 반지름이 5cm라고 할 때 이 원의 원주는 얼마인지 구하려면 어떻게 한다고요? 네 맞습니다. 원주는 지름 곱하기 원주율이라고 했죠. 그런데 우리가 지금 아는 건 반지름이죠. 지름은 반지름 곱하기 2니까 이걸로 대신 쓰고 곱하기 원주율이죠. 여기에 우리가 아는 숫자를 넣으면 반지름이 5cm고, 지름은 10cm가 되겠죠? 이 10에 3.1을 곱하면 31cm가 되죠? 이 31cm가 이 원의 원주가 되는 겁니다.

반대로 원주를 알면 지름도 알 수 있게되겠죠. 만약에 원주가 60cm인 원이 있다고 해보죠. 지름에 원주율을 곱해 원주를 구한다는 얘기는 원주를 원주율로 나누면 지름이 된다는 얘기잖아요. 이 원의 지름은 60을 원주율로 나누면 됩니다. 계산을 간단하게 하기 위해서 원주율을 반올림해서 3이라고 해보죠. 그럼 60 나누기 3을 하면 지름은 20이 나오죠. 즉, 이 원의 지름은 20cm라는 얘깁니다.

오늘은 이렇게 원의 지름과 원주의 관계에 대해서 알아봤습니다. 수고하셨습니다.
'초등수학' 카테고리의 다른 글
| 비례식과 비례배분 01 (6-2) (0) | 2022.09.09 |
|---|---|
| 비례식과 비례배분 01 (6학년) (0) | 2022.08.28 |
| 소수의 나눗셈 01 (6학년) (0) | 2022.08.15 |
| 분수의 나눗셈 02 (0) | 2021.02.27 |
| 분수의 나눗셈 01 (6학년) (0) | 2021.02.21 |



